Laplace Transforms Of The Derivatives

Laplace Transforms of the Derivatives:

If the Laplace Transform of f(t) is known then by using the following results we can find the Laplace transform of the derivatives;

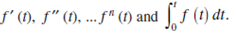
Laplace Transform of the derivatives: Function of exponential order. A continuous function f(t), t > 0 is said to be of exponential order.

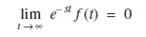
Theorem: If f(t) is exponential order and f' (t) is continuous then;

Proof: By the definition of Laplace Transform:

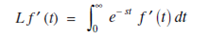
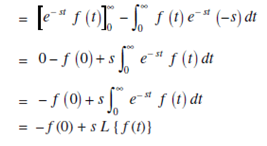
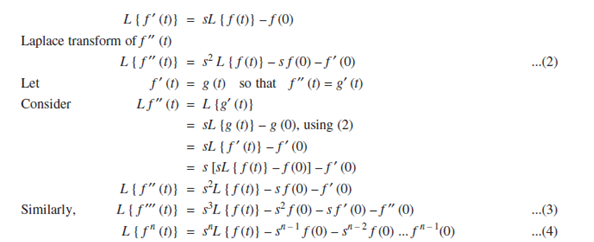
If f (t) = y then (4) can be written in the form:

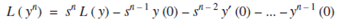
Where y' , y'' , ......... y⁽ⁿ⁾ denoted the sucessive derivatives.