Orthogonal Function Of Fourier Series

Orthogonal Function of Fourier Series: Basic Orthogonal Function used in Fourier Series are given as:

If we review the above example you will see that for each coefficients, if we wanted a_k, the coefficients of the k^th harmonic cosine, we multiplied the signals by  cos ( 2πkf₀t ). which translate the components of interest  to DC where it is extrated while discarding all other terms by integrating over exactly one cycle of the fundamental frequency. Similarly if we are interested in b_k, the coefficients of the k^th harmonic sine, we multiply the signal by sin ( 2πkf₀t ) which translate the components of interest to DC, where it is extracted while discarding all other terms by integrating over exactly one cycle of the fundamental frequency. This work because cos ( 2πkf₀t ) and sin ( 2πkf₀t ) are orthogonal functions, meaning that following orthogonality conditions are satiesfied by these functions.

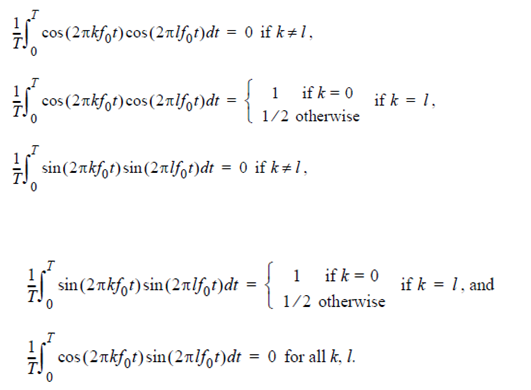
Thus if we multiply a T - periodic signals by either cos ( 2πkf₀t ) or sin ( 2πkf₀t ) and integrate over one cycle, we  isolate that components in the signals, contribution from all other components drop out of the results. Orthogonality implies that if there is a cos ( 2πkf₀t )components in a signal, it can only be represented by a_k in the Fourier series. In particular no other combination of coefficients could be used to represent that components. The same is true for a       sin ( 2πkf₀t )component and b_k. Thus orthogonality implies that the Fourier series of a waveform is unique.