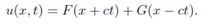Parabolic And Elliptic Equation With Constant Coefficients

Parabolic and Elliptic Equation with Constant Coefficients:

Parabolic:

The only solutions of main equations is;

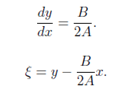
Again η is choosen judiciously but in such a way that the Jacobian of the transformation is not zero. Can A be zero in this case? In the parabolic case A = 0 implies B = 0. Therefore the original equations is;

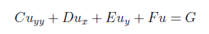
Which is canonical forms

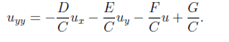
Elliptic:

Now we have complex conjucate functions ξ, η

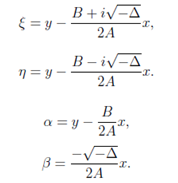
The canonical form is similar to the above equations.

Examples:

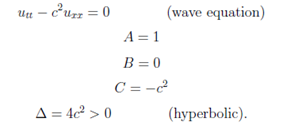
The charecristics equation is

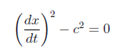
and the transformation is

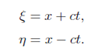
The solution in terms of x,t in the above equation we get;