Periodic Functions

Periodic Functions:

Periodic functions are functions which repeat: f (t P)= f (t) for all t. For example, if f (t) is the amount of time between sunrise and sunset at a certain latitude, as a function of time t, and P is the length of the year, then f (t P) = f (t) for all t, since the Earth and Sun are in the same position after one full revolution of the Earth around the Sun. We state this explicitly as the following definition: a function f (t) is periodic with period  P > 0  if,

          f (t P)= f (t)  for all t.

Example-1

f (x) = cos x

f (x 2π) = cos (x 2π)

= cos x cos2π - sin x sin 2π

= cos x

= f (x),  Hence cosx is periodic of period 2π.

Example-2

               f (x) = sin 4x

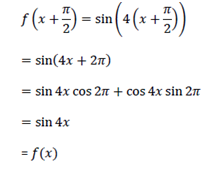
Hence sin nx is periodic of period π/2, observe that 2π is also a period of sin 4x.

Useful identification:

1. sin (ax b) = sin ax cosb cos ax sinb

2. cos (ax B) = cos ax cosb sin ax sinb

 

Functionality:

1. Any function can be considered periodic with period zero, this period is trivial and is not considered as a period.

2. If p is a period of f , then np is a period for any integer n.

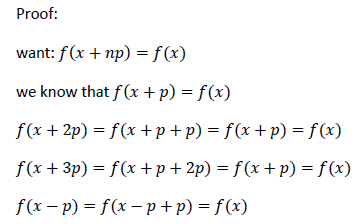
3. If p is a period then p/2 is not necessarily a period.

 

Fundamental Period:

The most interesting period for a periodic function is the smallest positive period , this period is called the Fundamental Period.

1. sin x is 2π

2. sin 3x is 2π/3