Properties Of The Fourier Series
Properties of the Fourier Series:
Basic properties of Fourier Series which are given as follows:
Linearity:
F is a linear transformation and so superposition holds. In other words, assume that a and b are simple real numbers, that x and y are T-periodic functions, and that

Symmetry:
1. Even waveforms:
A waveform x is even if x (t) = x (-t)
If x is also a T-periodic function and F (x) = X, then
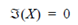 for all k.
for all k.
2. Odd Waveforms:
A waveform x is odd if x (t) = - x (-t)
If x is also a T-periodic function and F (x) = X, then
3. Real Waveforms:
If x is a real value T-periodic function and F (x) = X then
Xk = X-k * for all k. In other word, Xk equals the complex of X-k. As a result part of X is even and the imaginary part is odd.
Differentiation:
Let x be a T-periodic functions and
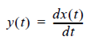
for all t. If F (x) = X and F (y) = Y, then
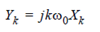 for all k.
for all k.
Integration:
Let x be a T-periodic functions and
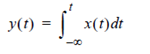
for all t. If F (x) = X and F (y) = Y, then
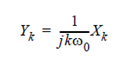
For all k. In this case X0 must be zero, otherwise the integral would not be a periodic function and its Fourier series would not exist.