Solution Of Linear Differential Equations

Solution of Linear Differential equations:

One of the important applications of Laplace transforms is to solve linear differential equations with constant coefficients with initial conditions. For example, consider a second order linear differential equations:

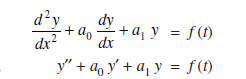
Taking Laplace transforms on both sides of the above equation and using the formulae on Laplace transforms of the derivatives y′ and y′′. We recall the formulae for immediate reference.

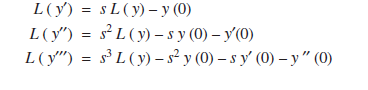
and so on.

Example:

(1) Solve using Laplace Transform.

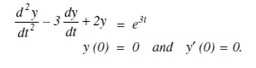
Solution: Given equation is y'' - 3y' 2y = e^3t

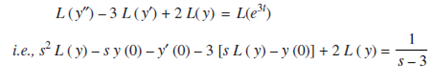
Where y (0) = 0 and y' (0) =0

Hence this is the required solutions.