Chi-square Test
Chi-Square Test:
Chi-square is a statistical test commonly used to compare observed data with data we would expect to obtain according to a specific hypothesis. For example, if, according to Mendel’s laws, you expected 10 of 20 offspring from a cross to be male and the actual observed number was 8 males, then you might want to know about the “goodness to fit” between the observed and expected. Were the deviations (differences between observed and expected) the result of chance, or were they due to other factors. How much deviation can occur before you, the investigator, must conclude that something other than chance is at work, causing the observed to differ from the expected. The chi-square test is always testing what null hypothesis, which states that there is no significant difference between the expected and observed result.
Chi-Square Distribution:
So for we discussed the sampling distribution of ¯ x, the sample mean. Now let us know about the sampling distribution of sample variance s2 when samples are randomly drawn from a normal population with mean μ and variance σ 2. Let x1, x2, ...xn be a sample of size n from the normal population, then the sampling distribution of the statistic
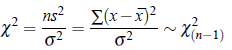
Here x2 (chi-square) is a statistic which has its distribution as x2 with (n−1) degrees of freedom. Another way of defining the x2 distribution is as follows: IF X1, X2, ...Xn are independent normal variates with mean μ and variance σ 2 then
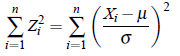
is distributed as x2 with n degrees of freedom. Symbolically.
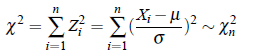
Some Properties of Chi-Square Distribution:
1. The distribution of x2 lies in the first quadrant.
2. The range of x2 distribution is from 0 to 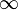 .
.
3. It has a unimodal curve.
4. x2 − distribution has only one parameter n which is its degrees of freedom (d.f).
5. The shape of the curve greatly vary as n varies.
6. The mean and variance of the x2 distribution with n d.f. are:
7. mean = n; variance = 2n