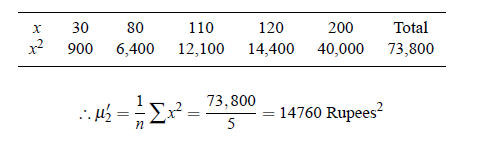Concept Of Moment
Moments about Any Arbitrary Point:
For an Individual Series In case of individual series x1,x2, . . . ,xn, rth moment about any arbitrary point a is denoted by μ′r and is defined as
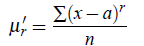
where r = 1,2,3,4,...
For an Frequency Distribution If x1,x2, . . . ,xn are the values of a variable x with the corresponding frequencies f1, f2, ..., fn respectively, then rth moment about any arbitrary point a is denoted by μ′r and is defined as
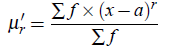
where r = 1,2,3,4,...
For an Frequency Distribution For grouped data, let x1,x2, . . . ,xn be taken as the mid- values then we have
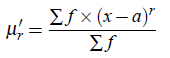
where r = 1,2,3,4,...
Standard Results:
1. Second moment about a is equal to mean square deviation about a., i.e. 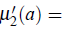
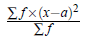
2. Second moment about mean is equal to variance, i.e. 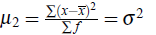
3. First moment about origin is mean, i.e. 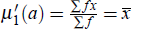
4. First moment about mean is always zero, i.e. 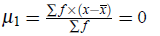
5. If the series is symmetrical about mean, then all the central moments are zero.
6. The value of a moment of order zero is always 1. i.e., 
Example: The amount in the pockets of 5 students in college were Rs.30,80,110,120 and 200 respectively. Find second moment about origin.
Solutions: