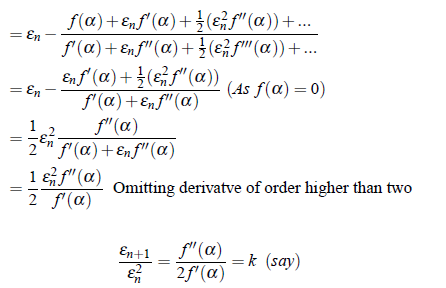Convergence Of Newton-raphson Method

Convergence of Newton-Raphson Method:

In this section, we will see the condition for the convergence of Newton-Raphson method. We have;

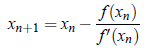
This is an iteration method where

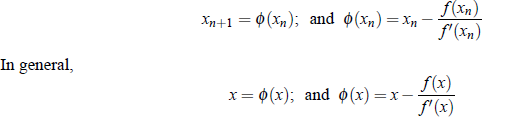
As iteration method converges for |Φ ′(x)| < 1, that is,

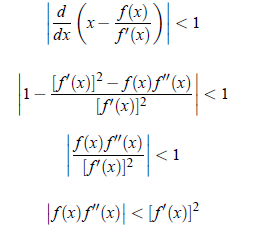
The interval containing the root α of f (x) = 0 should be selected in which the above is satisfied.

Rate Convergence of Newton-Raphson Method:

Let x_n and x_{n 1} be two successive approximations to the actual root a of f (x) = 0. Then

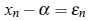
and

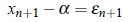
Fixed Point Iteration Method: In this method equation f (x) = 0 is written in the form of x = Φ (x), such that |Φ ′(x)| < 1. Then sequence generated by x_{n 1} = Φ (x_n) converges to the root of the equation f (x) = 0. where ei is the error in ith iteration;

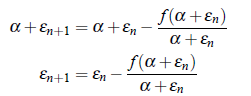
By Taylor’s Theorem