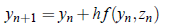Euler's Method

Euler's Method:

First Order Differential Equations:

Consider the differential equation;

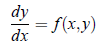
where y(x₀) = y₀.

Suppose that we wish to find successively y₁, y₂, ..., y_n where y_m is the value of y corresponding to x = x_m, where xm = x₀ mh, m = 1, 2, ...,h being small. Here, we use the property that in a small interval, a curve is nearly a straight line. Thus, in the interval x₀ to x₁ of x, we approximate the curve by the tangent at the point (x₀, y₀). Therefore, the equation of tangent at (x₀, y₀) is;

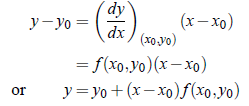
Hence, the value of y corresponding to x = x₁ is

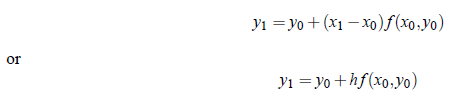
Since the curve is approximated by the tangent in [x₀, x₁], Equation above gives the approximated value of y₁.

Simialrly, approximating the curve int he next interval [x₁, x₂] by a line through (x₁, y₁) with slope f (x₁, y₁), we get;

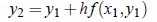
Proceeding on, in general it can be shown that

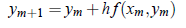
Simultaneous First Order Differential Equations:

Euler’s methed can be extended to the solution of system of ordinary differential equations. The folowing example illustrates the procedure.

Example: 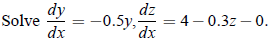using Euler’s method, assuming that x = 0, y = 4,and z = 6. Integrate to x = 2 with h = 0.5.

Solution: We have;

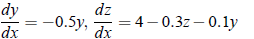
Euler’s formula is