Fitting An Exponential Curve
Fitting an Exponential Curve:
Consider the equation y = aebx. Taking on both sides, we get
log y = log a bx log e
so, Y = A Bx
Where Y = log y, A = log a and B = b log e.
This is equivalent to straight line fitting. Compute A and B from reduced normal equations
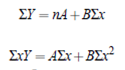
Finally compute a = antilog A and b = B/log e
Fitting a Power Function:
Consider the equation y = axb. Taking on both side we get;
log y = log a b log x
Y = A bX
Where Y = log y, A = log a and X = log x.
This is equivalent to straight line fitting. Compute A and B from reduced normal equations
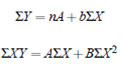
Example-1:
Determine the curve of the form y = axb.which is the best fit to the following data according to the least square principle:-

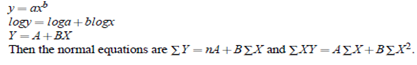
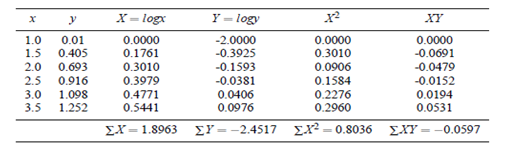
On putting these tabulated value in the normal equations we get;
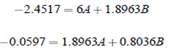
On solving we get;