Hurwitz Theorem

Hurwitz Theorem:

Suppose that { fn } is sequence in A (Ω) that coverges to f uniformly on compacts subsets of Ω. Let D (Zo,r) Ω and assume that f(z) ≠ 0 for [z - zo] = r. Then there is a positive integer N such that for n ≥ N, fn and f have same numbers of zeros in D (zo,r).

Proof : Let ε = 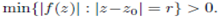Then for sufficiently large n,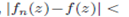 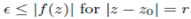. By Rouche theorem fn and f have the same numbers of zero in D (zo,r).

Theorem:

Let { fn } be sequence in A (Ω) such that fn → f uniformly on compact subset of Ω. If Ω is connected and fn has no zeros in Ω for infinitely many n, then either f has no zeros in Ω or f is identically zero.

Proof : Assume f is not identically zero but f has a zero at zo ∈ Ω. Then by the identity theorem there is r > 0 such that the hypothesis is satiesfied. Thus for sufficiently large n, fn has zero D (zo,r).

Theorem:

Let { fn } be a sequence in A (Ω) such that fn coverges to f uniformly on compact subset of Ω. If Ω is connected and the fn are one to one on Ω then either f is constant on Ω or f is one to one.

Proof : Assume that f is not constant on Ω and choose any zo ∈ Ω. The sequence { fn - fn(zo)} satiesfied the hypothesis of on the open connected set Ω/{zo}. Since f - f (zo) is not identically zero on Ω/zo. It follows from that f - f (zo) has no zero in Ω/{zo}. Since zo is an arbitrary point of Ω we conclude that f is one to one on Ω.

Definition:

A set 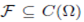is bounded if for each compact set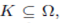 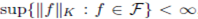That is the function in F are uniformly bounded on each compact subset of Ω. We will also require the notion of equicontinuity for a family of functions.

Definition:

A family of function F on Ωis equicontinuity at 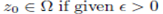there exists δ > 0 such taht if;

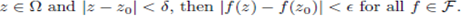
We have the following relationship between the bounded and equicontinuity subset of A (Ω).