Interpolation
Interpolation:
Interpolation is the process of finding a function whose graph passes through a set of given points. It is a method of constructing new data points within the range of a discrete set of known data points. In engineering and science one often has a number of data points, as obtained by sampling or experimentation, and tries to construct a function which closely fits those data points. This is called curve fitting or regression analysis. Interpolation is a specific case of curve fitting, in which the function must go exactly through the data points.
Finite Difference:
Let y = f (x) be a discrete function. Consider the given data set of n 1 values (x0, y0), (x1, y1), (x2, y2), ..., (xn, yn), where x differ by a quantity h, i.e. values of x are equidistant with interval distance h. The value of x is usually called argument and the corresponding function value y is called entry. In following subsection, we discuss three types of finite differences:
1. Forward Differences
2. Backward Differences
3. Central Differences.
Forward Differences:
For the given data set of n 1 values (x0, y0), (x1, y1), (x2, y2), ..., (xn, yn), the quantities y1 − y0, y2 − y1, ..., yn − yn−1 are called differences, particularly first differences, and are denoted by Δy0, Δy1, ..., Δyn−1 respectively. In general, first forward differences are given by;
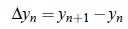
The symbol Δ is called forward difference operator. Further second forward differences are defined as the differences of the first differences. i.e.,
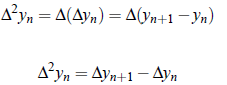
Here, Δ2 is called second forward difference operator. Similarly, other higher order forward difference may be computed. In general,
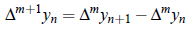
Forward Difference Table: