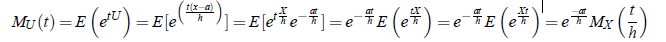Moment Generating Function
Moment Generating Function:
The function E(etX ) serves to generate moments of the probability distribution of the variate about the origin. and is called Moment Generating Function. The Moment Generating Function (m.g.f)of a random variable X(about origin) having the probability function f (x)
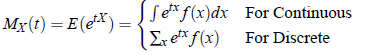
We consider for discrete distribution,
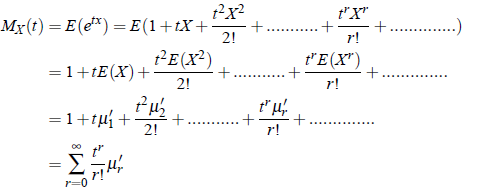
Similarly, we can show for continuous distribution. Thus rth moment of X about origin
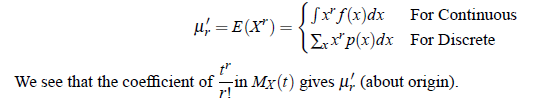
On differentiating above equation with respect to r and then putting t = 0 , we get;
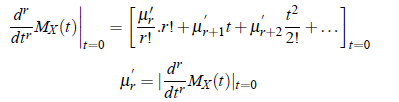
In general, the moment generating function X about the point X = a is defined as
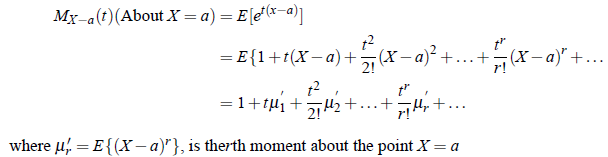
Properties of Moment Generating Functions:
1. McX (t) = MX (ct) c being constant.
2. If X1, X2, X3, ....................Xn are independent random variables, then the moment generating function of their sum X1 X2 ....... Xn is given by:
3. Effect of change of origin and scale on m.g.f: Let ustransform X to the new variable U by changing both the origin and scale in X as follows:
