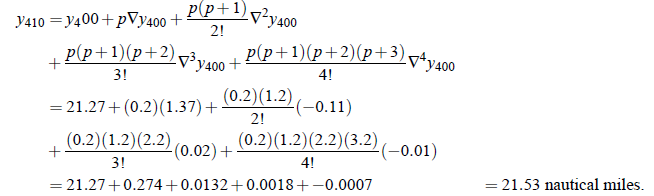Newton Backward Interpolation

Newton Backward Interpolation:

Let the function y = f (x) take the values y₀, y₁, y₂, ...,y_n corresponding to the values x₀, x₁, x₂, ...,x_n. Where x_i = x₀ ih, i = 0,1,2, ...,n. Suppose it is required to evaluate f (x) for the x = x₀ ph, where p is any real number.

We have for any real number p, we have defined E such that

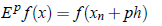
That is,

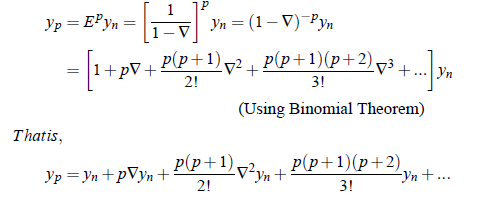
If y = f (x) is a polynimial of nth degree, then ^{n 1} and higher differences will be zero. Hence

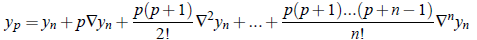
This formula is known as Newton’s Backward Formula.

Example: The table gives the distance in nautical miles of the visible horizon for the given height in feet above the earth’s surface:

Find the values of y when x = 410 ft.

Solution: The difference table is

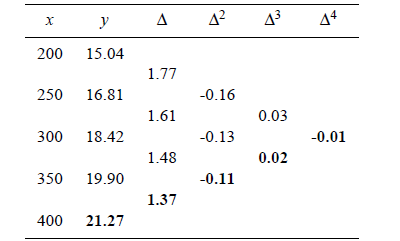
Since x = 400 is near the end of the table, we use Newton’s backward interpolation formula.

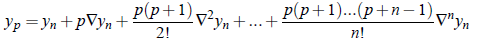
Thus required value;