Picard's Method

Picard's Method:

First Order Differential Equations:

Consider the first order differential equation;

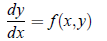
subject to y(x = x₀) = y₀. On integrating the above equation with respect to x between the limits (x₀, x), we get

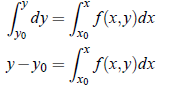
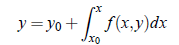
In Picard’s method, to obtain nth successive approximation, we write above equations as

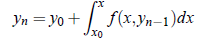
To terminate the process, we compare the values y_n and y_n−1 up to desired accuracy.

Simultaneous First Order Differential Equations:

Consider the simultaneous first order differential equation;

Piacrd’s successive approximation for these equation is;

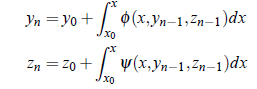
Using these equations, we may iterate the process up to desired accuracy of y and z.

Second Order Differential Equations:

Consider the second order differential equation;

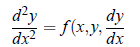
By putting dy/dz = z, the above equation reduces to first order simultaneous differential equations:

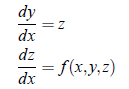
Now these equation can be solved as discussed in previous section.