Rate Of Convergence
Rate of Convergence:
Here, the speed at which a convergent sequence approaches its limit is called the rate of convergence. This concept is of practical importance if we deal with a sequence of successive approximations for an iterative method, as then typically fewer iterations are needed to yield a useful approximation if the rate of convergence is higher.
Convergence of A Sequence:
A sequence < xn > is said to be converges to α if for every ε > 0 there is an integer m > 0 such that if n > m then |xn − α| < ε . The number α is called the limit of the sequence and we sometimes write xn → c.
Convergence Speed for Iterative Methods:
Let < xn > be sequence of successive approximations of a root x = α of the equation f (x) = 0. Then the sequence < xn > is said to be converges to α with order q if
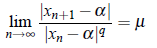
where μ > 0. Constant m is called the rate of convergence.
Particularly, if |xn 1 − α| = μ|xn − α|, n ≥ 0, 0 < μ < 1, then convergence is called linear or of first order. Convergence with order 2 is called quadratic convergence, and convergence with order 3 is called cubic convergence.
Examples: Find one of the real root of f (x) ≡ x6 − x − 1 = 0 accurate to within ε = 0.001.
Solution: We consider the interval [1,2], choose a = 1, b = 2; then f (a) = −1, f (b) = 61. This shows that condition 16.3 is satified for this interval. Now we may apply algorithm B1 to B3.
Iterations:1
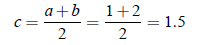
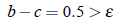
Move to next step, decide new interval
f (a). f (c) = (−1).(8.8906) = − 8.8906 < 0
This shows new interval [a, c] is valid interval. i.e. replace b = c. Now a = 1 and b = 1.5
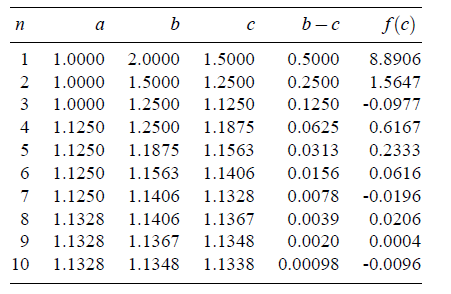
Iterations:2
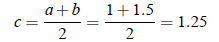
b − c = 0.25 > ε
Move to next step, decide new interval
f (a). f (c) = (−1).(1.5647) = −1.5647 < 0
This shows new interval [a, c] again, is a valid interval. i.e. replace b = c. Now a = 1 and b = 1.25 Note after 10th iteration b−c < ε . Stop iteration process at this step. Hence final approximated root is 1.1338.