Skewness
Skewness:
Skewness is a measure of the degree of asymmetry of a distribution. If the left tail ( Tail at small end of the distribution ) is more pronounced than the right tail ( Tail at the large end of the distribution ), the function is said to have negative skewness. If the reverse is true, it has positive skewness. If the two are equal, it has zero skewness.
Types of Skewness:
There are two types of skewness:
1. Positive Skewness
2. Negative Skewness
A distribution is said to be symmetrical if mean, median and mode are identical. If the distribution in which mean is maximum, mode is least and the median lies in between the two, is called a positively skewed distribution. While the distribution in which mode is maximum and mean is least and median lies in between the two, is called negatively skewed distribution. It is convention that skewness is said to be positive if the large tail of the distribution lies towards the higher values of the variables (as value of variables is always assumed increasing from left to right) and negative in the contrary.
Measure of Skewness:
Measures of skewness may be subjective (or abstract or absolute) or relative. Absolute measures tell us the direction and extent of asymmetry in a frequency distribution. Relative measures, often called coefficient of skewness, permit us to compare two or more frequency distributions. To compare two or more distributions the relative measure of skewness are used. these measures are as follows:
1. Karl Pearson’s coefficient of skewness:
2. Bowley’s coefficient of skewness:
3. Kelly’s coefficient of skewness:
4. Coefficient of skewness based on moments.
Karl Pearson’s Coefficient of Skewness:
It is denoted by Skp and is defined as:
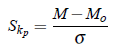
where M denotes mean, Mo denotes mode and s denotes standard deviation. In case of ill defined mode for some particular distribution, the value of empirical mode (Mo = 3Md −2M) is used in the formula. thus
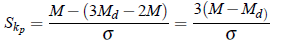
In both the cases, these coefficients are pure numbers since both numerator and denominator have the same dimensions. The value of the coefficient lies between -3 and 3. Again, if M = Md, then obviously, skewness is zero and this is interpreted as symmetrical distribution. If M > Mo or M > Md, then the skewness is positive, while if M < Mo or M < Md, then the skewness is negative.
Bowley’s Coefficient of Skewness:
It is defined as
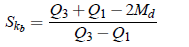
where Qrdenotes rth quartile and Md denotes median. The coefficients is pure number and lies between -1 and 1. The coefficient is positive or negative if Q3 Q1 > 2Md or Q3 Q1 < 2Md respectively. Again, it is zero if Q3 Q1 = 2Md, which shows the distribution is symmetric.
Kelly’s Coefficient of Skewness:
It is defined as
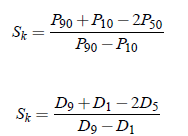
where Dr denotes rth decile and Pr denotes rth percentile.