Solution Of System Of Linear Equations
Solution of System of Linear Equations:
This chapter covers extremely important problem how to solve a large system of equations? The algebraic system of linear equations occur abundantly in various fields of science and engineering, like elasticity, electrical engineering ,fluid dynamics, heat transfer, structural analysis, statistics, biomedical engineering, vibration engineering and in control theory. A number of problems in numerical analysis can be reduced to, or approximated by, a system of linear equations.
One of the most common source of such systems is through discretization of ordinary or partial differential equations or integral equations. The system of n-linear equations in n-unknowns can be written as:
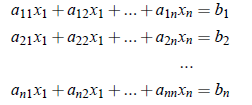
where the a’s are constant coefficients,the b’s are constants and n is the number of equations. The above system of linear equations may be expressed in a matrix notation as follows:
AX = B
where the coefficient matrix A is given by
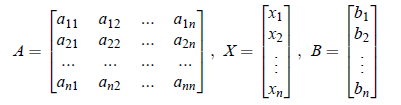
The augmented matrix is denoted as Af and is:
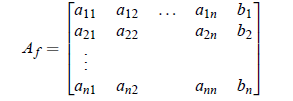
Here, one may note that if the rank of matrix A is less than the rank of matrix Af ,i.e, r(A) < r(Af ) then the system is said to be inconsistant. If r(A) = r(Af ),then the system is said to be consistant and has solution. We can find the solution of such equations by direct methods or iterative methods. Among the direct methods, we will discuss Crout’s method and in case of iterative methods, we will describe Gauss-seidel.