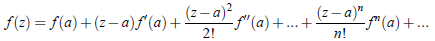Taylor Series

Taylor Series:

If function f (z) is analytic at all points inside a circle c, with its centre at the point a and radius R, then at each point z inside c,

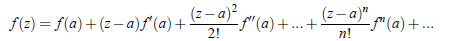
Proof: Let f (z) be analytic function within and on the circle circle c of radius r centered at a so that

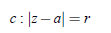
Draw another circle 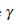: |z−a| = ρ, where ρ < r Hence by Cauchy’s integral formula, we have

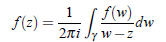
But,

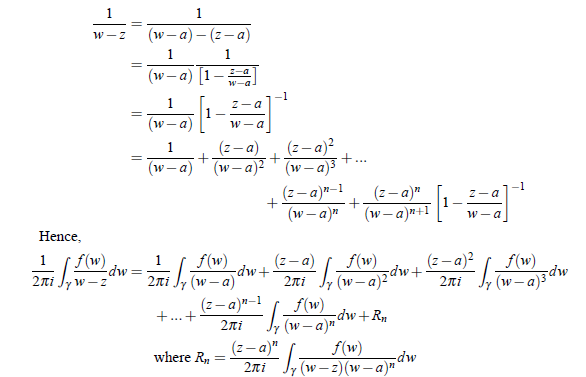
But, we have

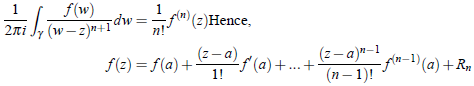
which is called Taylor’s formula, Rn being the remainder.

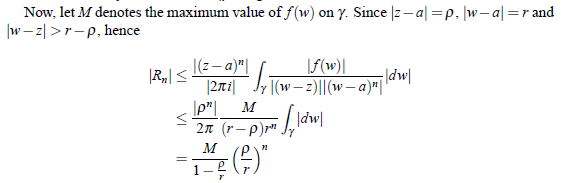
which tends to zero as n tends to infinity since ρ/r < 1. Thus