The Exponential Function

The Exponential Function:

We define the complex exponential as follows:

1. If z = x is real, then

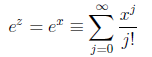
as in calculus. Here ! denotes “factorial”: j! = j·(j−1)·(j−2) · · · 3·2·1.

2. If z = iy is pure imaginary, then

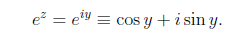
3. If z = x iy, then

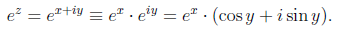
Part and parcel of the last definition of the exponential is the following complex-analytic definition of the sine and cosine functions:

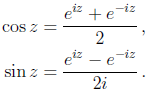
Note that when z = x i0 is real this new definition coincides with the familiar Euler formula from calculus:

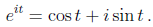
Exponential Using Power Series:

It is also possible to define the exponential using power series:

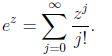
Either definition is correct for any z, and they are logically equivalent.

Laws of Exponentiation:

The complex exponential satisfies familiar rules of exponentiation:

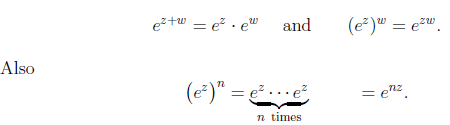
One may verify these properties directly from the power series definition, or else use the more explicit definitions in the above equations.