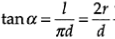Lead Screw And Nut Basic Equation

Lead screw and nut basic equation:

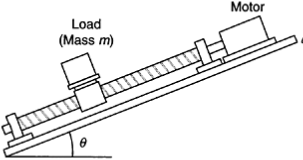
The basic equation for operation of a lead-screw drive is obtained now   suppose that a torque TR is provided by the screw at (and reacted by) the nut.

 Note that this is the net torque after deducting the inertia torque (due to inertia of the motor rotor and the lead screw) and the frictional torque of the bearings, from the motor (magnetic) torque. Torque TR is not completely available to move the load that is supported on the nut.

The reason is the energy dissipation (friction) at the screw and nut interface. Suppose that the net force available from the nut to drive the load in the axial direction is F.

 Denote the screw rotation by q and the rectilinear motion of the nut by x.

When the screw is rotated (by a motor) through 80, the nut (which is restrained from rotating due to the guides along which the support block moves) will move through dx along the axial direction.

The work done by the screw is TR.dq and the work done in moving the nut (with its load) is F.dx. The lead screw efficiency e is given by

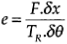
Now, rdq=dx, where the transmission parameter of the lead screw is r (axial distance moved per one radian of screw rotation). The “lead” l of the lead screw is the axial distance moved by the nut in one revolution of the screw, and it satisfies

l=2pr

In general, the lead is not the same as the “pitch” p of the screw, which is the axial distance between two adjacent threads. For a screw with n threads,

l=np

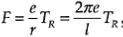
This result is the representative equation of a lead screw, and may be used in the design and selection of components in a lead-screw drive system.

For a screw of mean diameter d, the helix angle a is given by