Mechanical Elements

Mechanical Elements

For mechanical elements we use the velocity (across variable) of each independent mass (A-type element) and the force (through variable) of each independent spring (T-type element) as the system variables (state variables).

The corresponding constitutive equations form the “shell” for an analytical model. These equations will directly lead to a state-space model of the system,

Mass (Inertia) Element

The constitutive equation (Newton’s second law) is

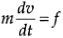
Since power =ƒu= rate of change of energy, by substituting, the energy of the element may be expressed as’

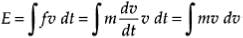
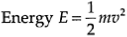
This is the well-known kinetic energy. Now by integrating, we have

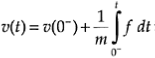
By setting t=0 in

U (0 ) =u (0- )

Unless an infinite force is applied to the mass element. Note that 0- denotes the instant just before t=0 and 0 denotes the instant just after t=0. In view of these observations, we may state the following:

1.       Velocity can represent the state of an inertia element. This is justified first because, the velocity at any time t can be completely determined with the knowledge of the initial velocity and the applied force, and because, from Equation 2.6, the energy of an inertia element can be represented in terms of u alone.

2.       Velocity across an inertia element cannot change instantaneously unless an infinite force/torque is applied to it.

3.       A finite force cannot cause an infinite acceleration in an inertia element. A finite instantaneous change (step) in velocity will need an infinite force. Hence, u is a natural output (or state) variable and ƒ is a natural input variable for an inertia element.