Microprocessor Numerical Control

Microprocessor Numerical Control

Fixed-Point Mathematics

The microprocessors in an embedded controller are generally quite small in comparison to a personal computer or computer workstation.

 Adding processing power in the form of a floating-point processor and additional RAM or ROM is not always an option. This means that sometimes the complex mathematical functions needed in a control system are not available.

However, sometimes the values being sensed and computed, though real numbers are of a reasonable range. Because of this situation there exists a special type of arithmetic whereby microcontrollers use integers in place of floating-point numbers to compute non-whole number (pseudo real) values.

There are several forms of fixed-point mathematics currently in use. The simplest form is based upon powers of 2, just like normal integers in binary.

However, a virtual binary point is inserted into the integer to allow an approximation of real values to be stored as integers. A standard 8-bit unsigned integer is shown below along with its equivalent decimal value.

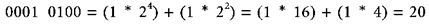
Suppose a virtual binary point is inserted between the two nibbles in the byte. There are now four bits left of the binary point with the standard positive powers of 2, and 4 bits right of the binary point with negative powers of 2. The same number now represents a real number in decimal.

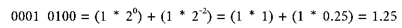
Rounding is sometimes necessary.

There is also a tradeoff in complexity, as the position of this virtual binary point must constantly be maintained when performing calculations.

The savings in memory usage and processing time, however, often overcome these tradeoffs; so fixed-point mathematics can be very useful.

Calibrations

The area of calibrating a system can sometimes take on an importance not foreseen when designing a mechatronic system. The use of calibrations, numerical and logical values kept in EEPROM or ROM; allow flexibility in system tuning and implementation.

 For example, if different microprocessor crystal speeds may be used in a mechatronic system, but real-time values are needed, a stored calibration constant of clock cycles per microsecond will allow this calculation to be affected. Thus, calibrations are often used as a gain, the value multiplied by some input in order to produce a scaled output. Also, as mentioned above, calibrations are often used in the testing of a mechatronic system in order to change the “feel” of the product.

A transmission control unit can use a set of calibrations on engine RPM, engine load, and vehicle speed to determine when to shift gears.

This is often done with hysteresis, as the shift points moving from second gear to third gear as from third gear to second gear may differ.