Modulation Theorem

Modulation Theorem

This is also known as the frequency-shifting theorem and relates the fact that if a signal is multiplied by a sinusoidal signal, the Fourier spectrum of the product signal is simply the Fourier spectrum of the original signal shifted through the frequency of the sinusoidal signal.

 In other words, the Fourier spectrum Xa(ƒ) of the amplitude-modulated signal xa(t) can be obtained from the Fourier spectrum X(ƒ) of the original data signal x(t) simply by shifting it through the carrier frequency ƒc.

To mathematically explain the modulation theorem, we use the definition of the Fourier integral transform to get

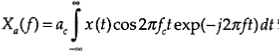
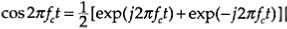
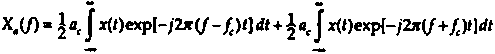
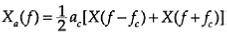
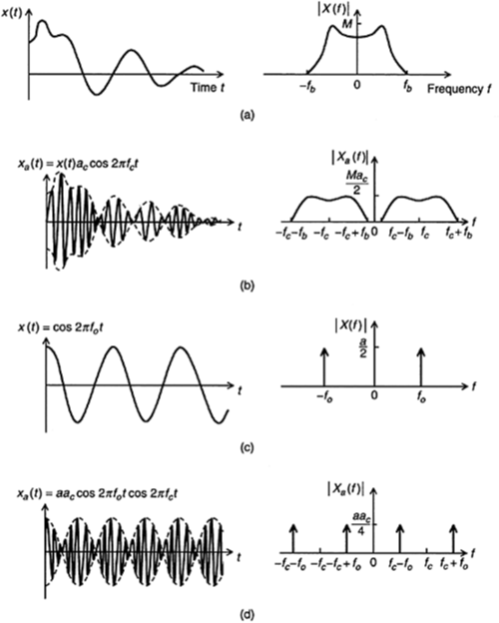
to amplitude modulate a high-frequency sinusoidal signal, the resulting modulated signal xa(t) and the magnitude of its Fourier spectrum .

 It should be kept in mind that the magnitude has been multiplied by ac/2. Furthermore, the data signal is assumed to be band limited, with bandwidth fb.

Of course, the theorem is not limited to band-limited signals, but for practical reasons, we need to have some upper limit on the useful frequency of the data signal.