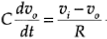Number Of Poles

Number of Poles

Analog filters are dynamic systems and they can be represented by transfer functions, assuming linear dynamics. Number of poles of a filter is the number of poles in the associated transfer function.

This is also equal to the order of the characteristic polynomial of the filter transfer function (i.e., order of the filter). Note that poles (or, eigenvalues) are the roots of the characteristic equation.

In our discussion we will show simplified versions of filters, typically consisting of a single filter stage. Performance of such a basic filter can be improved at the expense of circuit complexity (and increased pole count).

Only simple discrete-element circuits are shown for passive filters.

Basic operational-amplifier circuits are given for active filters. Even here, much more complex devices are commercially available, but our purpose is to illustrate the underlying principles rather than to provide complete descriptions and data sheets for commercial filters.

Low-Pass Filters

The purpose of a low-pass filter is to allow through all signal components below a certain (cutoff) frequency and block off all signal components above that cutoff.

Analog low-pass fitters are widely used as antialiasing filters in digital signal processing. An error known as aliasing will enter the digitally processed results of a signal if the original signal has frequency components above half the sampling frequency (half the sampling frequency is called the Nyquist frequency).

Hence, aliasing distortion can be eliminated if the signal is filtered using a low-pass filter with its cutoff set at Nyquist frequency, prior to sampling and digital processing.

 This is one of numerous applications of analog low-pass filters. Another typical application would be to eliminate high-frequency noise in a measured system response.

A single-pole passive low-pass filters circuit. An active filter corresponding to the same low-pass filter. It can be shown that the two circuits have identical transfer functions. Hence, it might seem that the op-amp is redundant. This is not true, however. If two passive filter stages are connected together, the overall transfer function is not equal to the product of the transfer functions of the individual stages.

The reason for this apparent ambiguity is the circuit loading (interaction) that arises due to the fact that the input impedance of the second stage is not sufficiently larger than the output impedance of the first stage.

But, if two active filter stages similar are connected together, such loading errors will be negligible because the op-amp with feedback (i.e., a voltage follower) introduces a very high input impedance and very low output impedance, while maintaining the voltage gain at unity.

With similar reasoning it can be concluded that an active filter has the desirable property of very low interaction with any other connected component. note that since the output is in open circuit (zero load current), the current through capacitor C is equal to the current through resistor R. Hence,