Resonance-type Band-pass Filters
Resonance-Type Band-Pass Filters
There are many applications where a filter with a very narrow pass band is required. The tracking filter mentioned in the beginning of the section on analog filters is one such application.
A filter circuit with a sharp resonance can serve as a narrow-band filter.
Note that the cascaded RC circuit shown in Figure does not provide an oscillatory response (filter poles are all real) and, hence, it does not form a resonance-type filter.
A slight modification to this circuit using an additional resistor R1 as shown in Figure (a) will produce the desired effect.
To obtain the filter equation, note that for the voltage follower unit
uA=uo
Next, since current through an op-amp lead is zero, for the high-pass circuit unit we have
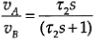
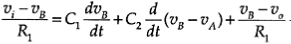
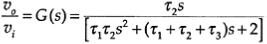
A low-pass Butterworth filter having 2 poles can provide a roll-off rate of -40 dB/decade and, one having 3 poles can provide a roll-off rate of -60 dB/decade.
Furthermore, the steeper the roll-off slope, the flatter the filter magnitude curves within the pass band.
A single-pole passive low-pass filters circuit. An active filter corresponding to the same low-pass filter. It can be shown that the
two circuits have identical transfer functions. Hence, it might seem that the op-amp is redundant.
This is not true, however. If two passive filter stages are connected together, the overall transfer function is not equal to the product of the transfer functions of the individual stages.
The reason for this apparent ambiguity is the circuit loading (interaction) that arises due to the fact that the input impedance of the second stage is not sufficiently larger than the output impedance of the first stage.
But, if two active filter stages similar are connected together, such loading errors will be negligible because the op-amp with feedback (i.e., a voltage follower) introduces a very high input impedance and very low output impedance, while maintaining the voltage gain at unity.