Robot Kinematics
Robot Kinematics
It is important to know the position and orientation (geometric configuration) of a robot, along with velocities and accelerations of the robot components (links) in order to monitor and properly control the robot.
Determination of these geometric configuration parameters and their derivatives is the kinematics problem of a robot. Coordinate transformation plays an important role in this problem.
Now we will address proper determination and representation of robot kinematics.
Each degree of freedom of a robotic manipulator has an associated joint coordinate qi. The robot is actuated by driving its joints, but a robotic task is normally specified in terms of end effector motions.
The end effector of a robot can be represented by a Cartesian coordinate frame fixed to it (a body frame). The frame can be represented as a coordinate transformation with respect to some inertial frame (the world coordinate frame), typically a frame fixed to the stationary base of the robot (the base frame).
The basic kinematics problem in modeling a robot is the expression of this coordinate transformation in terms of the joint coordinate’s qi.
Homogeneous Transformation
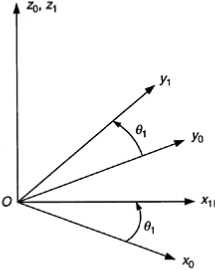
Consider the Cartesian frame (x0, y0, z0).
If this frame is rotated about the z0 axis through an angle q1, we get the Cartesian frame (x1y1, z1) as shown.
The coordinate transformation associated with this frame rotation may be represented by the