Spring (Stiffness) Element

Spring (Stiffness) Element

The constitutive equation (Hooke’s law) is

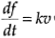
Note that we have differentiated the familiar force-deflection Hooke’s law, in order to be consistent with the response/state variable (velocity) that is used for the inertia element.

Now following the same steps as for the inertia element, the energy of a spring element may be expressed as

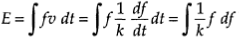
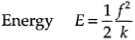
This is the well-known (elastic) potential energy. Also,

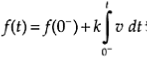
And

Ƒ(0 ) =ƒ (0- )

Unless an infinite velocity is applied to the spring element. In summary, we have

1.       Force can represent the state of a stiffness (spring) element. This is justified because the force of a spring at any general time t may be completely determined with the knowledge of the initial force and the applied velocity, and also because the energy of a spring element can be represented in terms of ƒ alone.

2.       Force through a stiffness element cannot change instantaneously unless an infinite velocity is applied to it.

3.       Force ƒ is a natural output (state) variable and u is a natural input variable for a stiffness element.