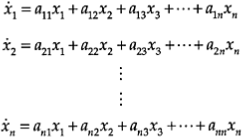State-space Representation

State-Space Representation

More than one variable might be needed to represent the response of a dynamic system. There also could be more than one input variable in a system.

 Then we have a multi-variable system. A time-domain analytical model is a set of differential equations relating the response variables to the input variables.

This set of system equations generally is coupled, so that more than one response variable appears in each differential equation.

 A particularly useful time-domain representation for a dynamic system is a state-space model. State equations define the dynamic state of a system. In the state-space representation, an nth-order system is represented by n first-order differential equations, which generally are coupled.

 An entire set of state equations is reduced to one vector-matrix State Equation.

State Space

The word “state” refers to the dynamic status or condition of a system.

A complete description of the state will require all the variables that are associated with the time evolution of the system response (both “magnitude” and “direction” of the response trajectory with respect to time).

The state is a vector, which traces out a trajectory in the state space. The analytical development requires a definition of the “state space.”

A second order system requires a two-dimensional or plane space, a third-order system requires a three-dimensional space, and so on.

State Equations

A common form of state equations for an nth-order linear, unforced (free, no input) system is