Auto-associative Memory Model - Hopfield Model
Introduction:-Auto-associative memory means patterns rather than associated pattern pairs, are stored in memory. Hopfield model is one-layer unidirectional auto-associative memory.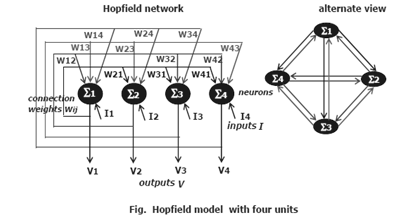
The model consists, a single layer of processing elements where each unit is connected to every other unit in the network but not to itself.
− Connection weight between or from neuron j to i is given by a number wij. The collection of all such numbers are represented by the weight matrix W which is square and symmetric, i.e, w i j = w j I for i, j = 1, 2. . . m.
− Each unit has an external input I which leads to a modification in the computation of the net input to the units as
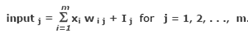
and xi is the ith component of pattern Xk
− each unit acts as both input and output unit. Like linear associator, a single associated pattern pair is stored by computing the weight matrix asWk =XkTWhere XK=YK
Weight Matrix : Construction of weight matrix W is accomplished by summing those individual correlation matrices, i.e.,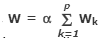 
where α is the constant of proportionality, for normalizing, usually set to 1/p to store p different associated pattern pairs. Since the Hopfield model is an auto-associative memory model, it is the patterns rather than associated pattern pairs, are stored in memory.
Decoding : After memorization, the network can be used for retrieval; the process of retrieving a stored pattern, is called decoding; given an input pattern X, the decoding or retrieving is accomplished by computing, first the net Input as
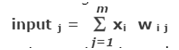
Where input j stands for the weighted sum of the input or activation value of node j , for j = 1, 2, ..., n. and xi is the i th component of pattern Xk , and then determine the units Output using a bipolar output function:
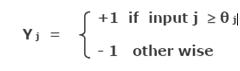
where θj is the threshold value of output neuron j .