Centers And Widths Of Rbf Neurons

Introduction:-It is obvious that the approximation accuracy of RBF networks can be increased by adapting the widths and positions of the Gaussian bells in the input space to the problem that needs to be approximated. There are several methods to deal with the centers c and the widths of the Gaussian bells:

Fixed selection: The centers and widths can be selected in a fixed manner and regardless of the training .

Conditional, fixed selection: Again, centers and widths are selected fixedly, but we have previous knowledge about the functions to be approximated and comply with it.

Adaptive to the learning process: This is definitely the most elegant variant, but certainly the most challenging one, too.

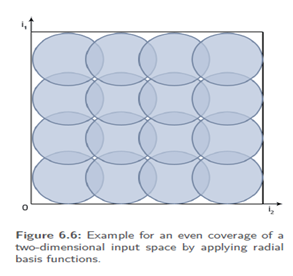Fixed selection:-The goal is to cover the input space as evenly as possible. Here, widths of 2/ 3 of the distance between the centers can be selected so that the Gaussian bells overlap by approx. "one third". The closer the bells are set the more precise but the more time-consuming the whole thing becomes. This may seem to be very in elegant, but in the field of function approximation we cannot avoid even coverage. Here it is useless if the function to be approximated is precisely represented at some positions but at other positions the return value is only 0. However, the high input dimension requires a great many RBF neurons, which increases the computational effort exponentially with the dimension and for the fact that six- to ten dimensional problems in RBF networks are already called "high-dimensional".

Conditional, fixed selection:-Suppose that our training samples are not evenly distributed across the input space. It then seems obvious to arrange the centers and sigma of the RBF neurons by means of the pattern distribution. So the training patterns can be analyzed by statistical techniques such as a cluster analysis, and so it can be determined whether there are statistical factors according to which we should distribute the centers and stigmas’ more trivial alternative would be to set |H| centers on positions randomly selected from the set of patterns. So this method would allow for every training pattern p to be directly in the center of a neuron. This is not yet very elegant but a good solution when time is an issue. Generally, for this method the widths are fixedly selected. If we have reason to believe that the set of training samples is clustered, we can use clustering methods to determine them. There are different methods to determine clusters in an arbitrarily dimensional set of points.

Another approach is to use the approved methods: We could slightly move the positions of the centers and observe how our error function Err is changing – a gradient descent, as already known from the MLPs.