Combinations Of Equation System And Gradient Strategies

Description:-Analogous to the MLP we perform a gradient descent to find the suitable weights by means of the already well known delta rule. Here, back propagation is unnecessary since we only have to train one single weight layer, which requires less computing time.

We know that the delta rule is

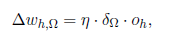
In which we now insert as follows:

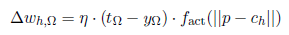
Here again I explicitly want to mention that it is very popular to divide the training into two phases by analytically computing a set of weights and then refining it by training with the delta rule. There is still the question whether to learn offline or online. Here, the answer is similar to the answer for the multilayer perceptron: Initially, one often trains online (faster movement across the error surface).Then, after having approximated the solution, the errors are once again accumulated and, for a more precise approximation, one trains offline in a third learning phase. However, similar to the MLPs, you can be successful by using many methods. As already indicated, in an RBF network not only the weights between the hidden and the output layer can be optimized. So let us now take a look at the possibility to vary σ and c.