Competitive Learning Neural Networks
Introduction:-While no information is available about desired outputs the network updated weights only on the basis of input patterns. The Competitive Learning network is unsupervised learning for categorizing inputs. The neurons (or units) compete to fire for particular inputs and then learn to respond better for the inputs that activated them by adjusting their weights.
An example of competitive learning network is shown below.
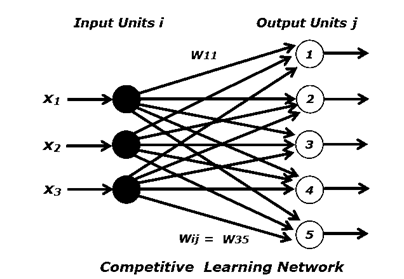
– All input units i are connected to all output units j with weights Wij .
– Number of inputs is the input dimension and the number of outputs is equal to the number of clusters that data are to be divided into.
– The network indicates that the 3-D input data are divided into 5 clusters.
– A cluster center position is specified by the weight vector connected to the corresponding output unit.
– The clusters centers, denoted as the weights, are updated via the competitive learning rule.
– For an output unit j , the input vector X = [x1 , x2 , x3 ]T and the weight vector Wj = [w1j , w1j , w1j ]T are normalized to unit length.
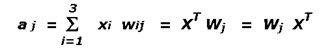
– The activation value aj of the output unit j is calculated by the inner product of the weight vectorsand then the output unit with the highest activation is selected for further processing; this implied competitive.
– Assuming that output unit k has the maximal activation, the weights leading to this unit are updated according to the competitive, called winner-take-all (WTA) learning rule which is normalized to ensure that wk (t 1) is always of unit length; only the weights at the winner output unit k are updated and all other weights remain unchanged.
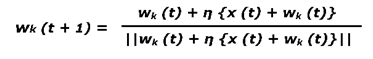
– Alternately, Euclidean distance as a dissimilarity measure is a more general scheme of competitive learning, in which the activation of output unit j is as
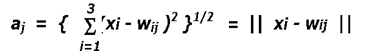
the weights of the output units with the smallest activation are updated according to
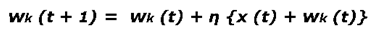
A competitive network, on the input patterns, performs an on-line clustering process and when complete the input data are divided into disjoint clusters such that similarity between individuals in the same cluster are larger than those in different clusters. Stated above, two metrics of similarity measures: one is Inner product and the other Euclidean distance. Other metrics of similarity measures can be used. The selection of different metrics leads to different clustering.