Encoding The Information

Introduction:-Two possible ways of representing knowledge in neural networks are (1) local representation, where every neuron represents one concept or one variable, etc., and

(2) distributed representation, where a concept or a value for a variable is represented by the collective activation of a group of neurons.

Each way has alternatives. For example, we can represent an output variable that has the context of "percentage" as one neuron (activation values from 0 to 1, a value of 0.01 corresponding to 1%, etc.).Another possible neuronal encoding may use 10 neurons for a "thermometer" encoding (the first neuron represents percentage from 0% to 10%, the second, from 10% to 20%, etc., 100% being represented by the activation of all the output neurons).

When MLP with logistic activation function is used, the output (target) values o are usually chosen in the interval [0.1,0.9] rather than in [0.0, 1.0] as the derivative of the logistic function which is o(1-o) has a value of 0.0 for o = 0.0 and o = 1.0.

Output activation values can be interpreted differently, depending on the context of the problem, eitheras a kind of probability for an event to happen, or as a kind of certainty, confidence, or degree of an event that has happened but only in part, or simply as a value of an output variable.

Encoding the input information is sometimes difficult. This can be caused by problems such as missing values for some of the variables, and unknown dependencies between the problem variables and difficulties in choosing the appropriate set of features. This is the problem with the feature space. Should it be large, or can a better solution be achieved if a smaller number of input variables are used, thereby achieving a smaller problem space?

There are some approaches to solving the first problem. For example, the data instances (training examples) with missing information can be omitted if there are enough other examples. But a better solution may be obtained if the missing values are substituted by the mean value for the corresponding variable over the whole data set.

The second problem seems to be more difficult. Too many variables require much space and time (for training) and may be the cause of a degraded solution due to the introduction of noise through redundant variables and their (possibly) numerous values. Too small a number of variables may not carry sufficient information for solving the problem.

One possible solution to this problem is to analyze the sensitivity (Si) of the neural network to individual variables, say xi. In this case all the values for xi in the training data set are substituted with the mean valueM_xifor xi, and for each individual example j = 1, 2, . . ., p, the error E(M(xi)) is compared to the error E(x_ij) when xi is used with its real value x_ij:

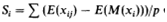
Variables with small sensitivity are deleted from the data set, which will increase the speed of training and reduce the size of the network. Some techniques are often used when preparing data for training a neural network, one of them being

normalization. The neuronal input signals may be normalized into the same scope, usually in the interval of [0, 1], or [-1, 1]. This makes all the neuronal inputs of equal importance.

Actually, input data to a neural network represent values of a set of features. What features to use depends on the task and the goals. One possibility is to use fuzzy representation (transformation) or real data as input features of neural networks. Using fuzzified data for training neural networks has the following advantages:

Faster training and better generalization.
Easier rules extraction and network interpretation.
Fuzzy labels are extra information (knowledge), which may lead to a better solution.
It is easy to adjust fuzzy labels according to new situations, thus making the whole system adaptable to new circumstances.

For example, 30 years ago, a weekly wage of $400 was considered to be "good", now it is "low." So, using "old" data is still possible but appropriately labeled.