Exemplary Problems Allow For Testing Self-coded Learning Strategies

Introduction:-Looking at a few exemplary problems which we  can use later to test implemented networks and learning rules.

1.Boolean functions:-A popular example is the one that did not work in the nineteen-sixties: the XOR function. We need a hidden neuron layer,. Thus, we need at least two neurons in the inner layer. Let the activation function in all layers be the hyperbolic tangent.

Trivially, we now expect the outputs 1.0or −1.0, depending on whether the function XOR outputs 1 or 0 - and exactly here is where the first beginner’s mistake  occurs. For outputs close to 1 or -1, i.e. close to the limits of the hyperbolic tangent, we need very large network inputs. The only chance to reach these network inputs are large weights, which have to be learned: The learning process is largely extended. Therefore it is wiser to enter the teaching inputs 0.9 or −0.9 as desired outputs or to be satisfied when the network outputs those values instead of 1 and −1.

2.The parity function:-The parity function maps a set of bits to 1or 0, depending on whether an even number of input bits is set to 1 or not. Basically, this is the function 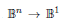.It is characterized by easy learnability up to approx. n = 3, but the learning effort rapidly increases from n = 4. The reader may create a score table for the 2-bit parity function.

3.The 2-spiral problem:-As a training sample for a function let us take two spirals coiled into each other with the function certainly representing a mapping 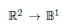.One of the spirals is assigned to the output value 1, the other spiral to 0. Here, memorizing does not help. The network has to understand the mapping itself.

4.The checkerboard problem:-Create a two-dimensional function Of the form 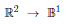and specify checkered training samples with one colored field representing 1 and all the rest of them representing 0. The difficulty increases proportionally to the size of the function: While a 3×3 field is easy to learn, the larger fields are more difficult. The 2-spiral problem is very similar to the checkerboard problem, only that, mathematically speaking, the first problem is using polar coordinates instead of Cartesian coordinates.