Fuzzy Operations

A fuzzy set operations are the operations on fuzzy sets. The fuzzy set  operations are generalization of crisp set operations. The fuzzy set theory in the terms of standard operations: Complement,   Union,    Intersection,   and    Difference.

The graphical interpretation of  the  following  standard fuzzy set terms  and  the  Fuzzy Logic  operations  are  illustrated: 

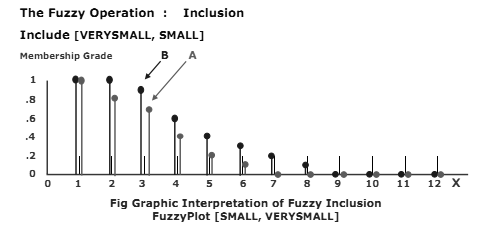
 Inclusion  :  FuzzyInclude [VERYSMALL, SMALL] 

Equality :    FuzzyEQUALITY [SMALL, STILLSMALL] 

Complement  :  FuzzyNOTSMALL = FuzzyCompliment [Small]

Union :  FuzzyUNION = [SMALL  ∪  MEDIUM] 

Intersection  :  FUZZYINTERSECTON = [SMALL  ∩  MEDIUM]

Inclusion :-Let  A  and  B  be  fuzzy sets defined in the same universal space  X.  The fuzzy set A is included in the fuzzy set B  if and only if  for every x in the set X we have A(x) ≤  B(x)

Example :   The  fuzzy  set  UNIVERSALSPACE  numbers,  defined   in   the   universal space  X = { xi } = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}   is presented as  SetOption [FuzzySet,  UniversalSpace → {1, 12, 1}] 

 The fuzzy set B  SMALL

The Set  SMALL  in set  X  is :  SMALL =  FuzzySet {{1, 1   },   {2, 1  },  {3, 0.9},   {4, 0.6},   {5, 0.4},  {6, 0.3}, {7, 0.2},     {8, 0.1},    {9, 0  },  {10, 0 },   {11, 0},    {12, 0}}

Therefore SetSmall   is represented as  SetSmall = FuzzySet [{{1,1},{2,1}, {3,0.9}, {4,0.6}, {5,0.4},{6,0.3}, {7,0.2}, {8, 0.1}, {9, 0},  {10, 0}, {11, 0}, {12, 0}} , UniversalSpace → {1, 12, 1}]

The fuzzy set  A  VERYSMALL

The Set  VERYSMALL  in set X  is :  VERYSMALL =  FuzzySet {{1, 1   },   {2, 0.8  },  {3, 0.7},   {4, 0.4},   {5, 0.2},  {6, 0.1},  {7, 0 },     {8, 0 },    {9, 0  },  {10, 0 },   {11, 0},    {12, 0}}

Therefore SetVerySmall  is represented as  SetVerySmall = FuzzySet [{{1,1},{2,0.8}, {3,0.7}, {4,0.4}, {5,0.2},{6,0.1},  {7,0}, {8, 0}, {9, 0},  {10, 0}, {11, 0}, {12, 0}} , UniversalSpace → {1, 12, 1}]

Comparability :-Two fuzzy sets  A  and  B  are comparable 

if the condition  A ⊂ B or B ⊂ A  holds,  i.e.,  

if one of the fuzzy sets is a subset of the other set, they are comparable.

Two fuzzy sets A and B are incomparable 

If the condition  A ⊄ B or B ⊄ A  holds.

Example 1:

Let    A = {{a, 1}, {b, 1}, {c, 0}}    and   B = {{a, 1}, {b, 1}, {c, 1}}. 

Then A  is  comparable  to  B,  since  A  is   a subset  of  B.

Example 2 : 

Let    C = {{a, 1}, {b, 1}, {c, 0.5}} and D = {{a, 1}, {b, 0.9}, {c, 0.6}}. 

Then C and D are not comparable since C is not a subset of D  and  D is not a subset of C.