Fuzzy Systems
Introduction:-Fuzzy Systems include Fuzzy Logic and Fuzzy Set Theory.
• Knowledge exists in two distinct forms :
− The Objective knowledge that exists in mathematical form is used in engineering problems; and
− The Subjective knowledge that exists in linguistic form, usually impossible to quantify.
Fuzzy Logiccan coordinate these two forms of knowledge in a logical way.
• Fuzzy Systems can handle simultaneously the numerical data and linguistic knowledge.
• Fuzzy Systems provide opportunities for modeling of conditions which are inherently imprecisely defined.
• Many real world problems have been modeled, simulated, and replicated with the help of fuzzy systems.
• The applications of Fuzzy Systems are many like: Information retrieval systems, Navigation system, and Robot vision.
• Expert Systems design has become easy because their domains are inherently fuzzy and can now be handled better.
Examples: Decision-support systems, financial planners, Diagnostic system, and Meteorological system.
Any system that uses Fuzzy mathematics may be viewed as Fuzzy system.
The Fuzzy Set Theory- membership function, operations, properties and the relations have been described in previous lectures. These are the prerequisites for understanding Fuzzy Systems. The applications of Fuzzy set theory is Fuzzy logic which is covered in this section. Here the emphasis is on the design of fuzzy system and fuzzy controller in a closed–loop. The specific topics of interest are:
− Fuzzification of input information,
− Fuzzy Inferencing using Fuzzy sets,
− De-Fuzzification of results from the Reasoning process, and
− Fuzzy controller in a closed–loop.
Fuzzy Inferencing, is the core constituent of a fuzzy system. A block schematic of Fuzzy System is shown in the next slide. Fuzzy Inferencing combines the facts obtained from the Fuzzification with the fuzzy rule base and conducts the Fuzzy Reasoning Process.
Fuzzy System elements
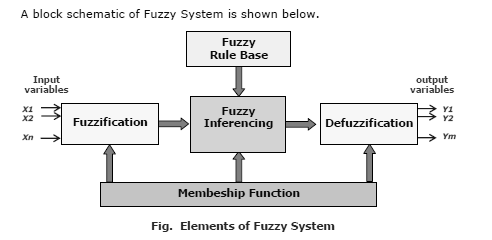
− Input Vector : X = [x1 , x2, . . . xn ] T are crisp values, which are transformed into fuzzy sets in the fuzzification block.
− Output Vector : Y = [y1 , y2, . . . ym ] T comes out from the defuzzification block, which transforms an output fuzzy set back to a crisp value.
− Fuzzification : a process of transforming crisp values into grades of membership for linguistic terms, "far", "near", "small" of fuzzy sets.
− Fuzzy Rule base : a collection of propositions containing linguistic variables; the rules are expressed in the form:
If (x is A ) AND (y is B ) . . . . . . THEN (z is C) where x, y and z represent variables (e.g. distance, size) and A, B and Z are linguistic variables (e.g. `far', `near', `small').
− Membership function : provides a measure of the degree of similarity of elements in the universe of discourse U to fuzzy set.
− Fuzzy Inferencing : combines the facts obtained from the Fuzzification with the rule base and conducts the Fuzzy reasoning process.
− Defuzzyfication: Translate results back to the real world values.