Hebbian Learning Rule

Introduction:-In 1949, Donald O. Hebb formulated the Hebbian rule which is the basis for most of the complicated learning rules.

Original rule:-Hebbian rule"If neuron j receives an input from neuron i and if both neurons are strongly active at the same time, then increase the weight w_i,j.

Mathematically speaking, the rule is:

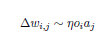
with 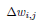being the change in weight from i to j , which is proportional to the following factors:

• The output o_i of the predecessor neuron i, as well as,
• The activation a_j of the successor neuron j
• A constant η, i.e. the learning rate

Hebb postulated his rule long before the specification of technical neurons. Considering that this learning rule was preferred in binary activations, it is clear that with the possible activations (1, 0) the weights will either increase or remain constant. Sooner or later they would go ad infinitum, since they can only be corrected "upwards" when an error occurs. This can be compensated by using the activations (-1,1)². Thus, the weights are decreased when the activation of the predecessor neuron dissents from the one of the successor neuron, otherwise they are increased.

Generalized form:-Mathematically more general form of the Hebbian rule.

The generalized form of the Hebbian Rule only specifies the proportionality of the change in weight to the product of two undefined functions, but with defined input values.

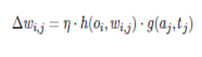
Thus, the product of the functions

• g(a_j , t_j) and
• h(o_i,w_i,j)
• as well as the constant learning rate η

Results in the change in weight,h receives the output of the predecessor cell o_i as well as the weight from predecessor to successor w_i,j while g expects the actual and desired activation of the successor a_j and t_j.