Learning Vector Quantization Algorithms For Supervised Learning
Introduction:-The problem of distinguishing input vectors that "fall" in the bordering area between two output neurons and the necessity for using known labels of the neurons for better topological mapping of the input vectors into the output space have led to the development of learning vector quantization (LVQ) algorithms LVQ1, LVQ2, and LVQ3 (Kohonen 1990).
LVQ1 AlgorithmIn LVQ1 several codebook vectors are assigned to each class, and each is labeled with the corresponding class symbol (label). Initial values of the codebook vectors are learned by the SOM algorithm.
The output neurons are then labeled according to the classes. Then a correction of the weights with the use of the known labels is performed by applying the following formulas to update the weights vectors:
wj(t 1) = wj(t) a(t)(x(t) - wj(t)),if x is classified by the network correctly in class cjrepresented by the jth neuronwj(t 1) = wj(t) - a(t)(x(t) - wj(t)),if x has been wrongly associated by the network with class-neuron j
wi(t 1) = wi(t), for all i different form j a(t) is a scalar gain factor which decreases monotonically in time.
LVQ2 AlgorithmIn the LVQ2 algorithm, a further tuning of the weights of the immediate neighbors to the winning neuron, after a presentation of an input vector, is done. If, for example, ci is the class of the winning neuron, but x belongs to the class cjof its neighbor j, the following formulas are applied to calculate the new weight vectors for neurons i and j:-
wi(t 1) = wi(t) - a(t)(x(t) - wi(t)), or
wj(t 1) = wj(t) a(t)(x(t)- wj(t)), or
wk(t 1) = wk(t), for the rest of the neurons k
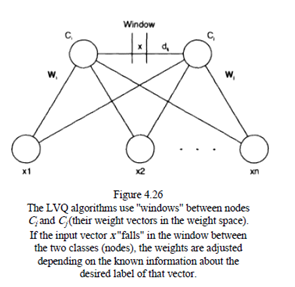
LVQ3 AlgorithmIn the LVQ3 algorithm a window between the lateral output neurons i and j is considered. When the input vector x falls out of the window, it is the LVQ2 algorithm which determines one of the i or j neurons to be a winner and updates the new codebook vectors. But if the input vector x falls in the window, then other formulas are applied:
wi(t 1) = wi(t) - a(t)(x(t) - wi(t)),if x falls in the "window" and x belongs to classcj
wj(t 1) = wj(t) a(t)(x(t) - wj(t)),for k Î {i, j}, if x falls in the "window" and x belongs to class cj
wk(t 1) = wk(t) a(t)(x(t) - wk(t)),for k Î {i, j}, if x falls in the window and i and j represent the same class.