Model Of A Neuron

Introduction:-A neuron is an information-processing unit that is fundamental to the operation of a neural network. The model of a neuron, which forms the basis for designing neural networks. Here we identify three basic elements of the neuronal model:-

1. A set of synapses or connecting links, each of which is characterized by a weight or strength of its own. Specifically, a signal Xj a t the input of synapse j connected to neuron k is multiplied by the synaptic weight wkj" It is important to make a note of the manner in which the subscripts of the synap tic weight wkj are written. The first subscript refers to the neuron in ques tion and the second subscrip t refers to the input end of the synapse to which the weight refers. Unlike a synapse in the brain, the synaptic weight of an artificial neuron may lie in a range that includes negative as well as positive values.

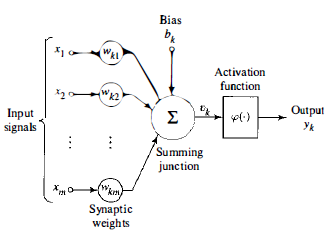
2.An adder for summing the input signals, weighted by the respective synapses of the neuron; the operations described here constitute a linear combiner.

3. An activation function for limiting the amplitude of the output of a neuron. The activation function is also referred to as a squashing function in that it squashes the permissible amplitude range of the output signal to some finite value.

Typically, the normalized amplitude range of the output of a neuron is written as the closed unit interval [0, 1] or alternatively [- 1, 1]. The neuronal model also includes an externally applied bias, denoted by b_k.The bias b_k has the effect of increasing or lowering the net input of the activation function,depending on whether it is positive or negative, respectively.In mathematical terms, we may describe a neuron k by writing the following pair of equations:

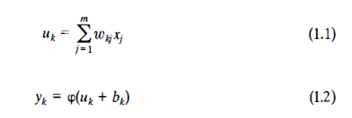
Where the input signals are\are the synaptic weights of neuron k; U_kis the linear combiner output due to the input signals; b_kis the bias;is the activation function; and Y_kis the output signal of the neuron. The use of bias b_khas the effect of applying an affine transformation to the output U_kof the linear combiner depends on whether the bias b_k is positive or negative, the relationshipbetween the induced local field or activation potential V_k of neuron k and the linear combiner output U_k is modified; hereafter the term "induced local field" is used. Note that as a result of this affine transformation, the graph of V_k versus U_k no longer passes through the origin.

The bias b_k is an external parameter of artificial neuron k. We may account for its

In particular, depending on whether the bias b_k is positive or negative, the relationship between the induced local field or activation potential V_kof neuron k and the linear combiner output U_kis modified in the manner; hereafter the term "induced local field" is used. Note that as a result of this affine transformation, the graph of V_kversus U_kno longer passes through the origin. The bias b_kis an external parameter of artificial neuron k. We may account for its presence as in Eq. (1.2). Equivalently, we may formulate the combination of Eqs. (1.1)to (1.3) as follows:

In Eq. (1.4) we have added a new synapse. Its input is

And its weight is,