Neural Network As A Directed Graph
Introduction:- The presence of nonlinearity in the model of a neuron limits the scope of their application to neural networks . Nevertheless, signal-flow graphs do provide a neat method for the portrayal of the flow of signals in a neural network. A signal-flow graph is a network of directed linksthat are interconnected at certain points called nodes. A typical node j has an associated node signal xj"
A typical directed link originates at node j and terminates on node k; it has an associated transfer function or transmittance that specifies the manner in which the signal Ykat node k depends on the signal Xj at node j.The flow of signals in the various parts of the graph is dictated by three basic rules:
Rule 1. A signal flows along a link only in the direction defined by the arrow on the link.
Two different types of links may be distinguished:
• Synaptic links, whose behavior is governed by a linear input-output relation. Specifically, the node signal Xi is multiplied by the synaptic weight w" to produce the node signal Yk.
• Activation links, whose behavior is governed in general by a nonlinear input output relation.
Rule 2. A node signal equals the algebraic sum of all signals entering the pertinent node via incoming link&This second rule is for the case of synaptic convergence or fan-in.
Rule 3. The signal at a node is transmitted to each outgoing link originating from that node, with the transmission being entirely independent of the transfer functions of theoutgoing links.
Mathematical definition of a neural network:-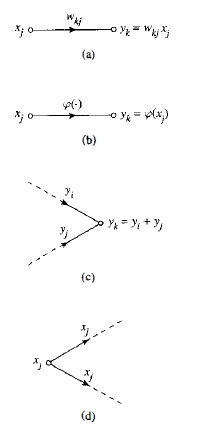
A neural network is a directed graph consisting of nodes with interconnecting synaptic and activation links, and is characterized by four properties:
- Each neuron is represented by a set of linear synaptic links, an externally applied bias, and a possibly nonlinear activation link. The bias is represented by a synaptic link connected to an input fixed at l.
- The synaptic links of a neuron weight their respective input signals.
- The weighted sum of the input signals defines the induced local field of the neuron in question.
- The activation link squashes the induced local field of the neuron to produce an output.
The state of the neuron may be defined in terms of its induced local field or its output signal. A directed graph so defined is complete in the sense that it describes not only the signal flow from neuron to neuron, but also the signal flow inside each neuron. When, however, the focus of attention is restricted to signal flow from neuron to neuron, we may use a reduced form of this graph by omitting the details of signal flow inside the individual neurons. Such a directed graph is said to be partially complete. It is characterized as follows:-
1. Source nodes supply input signals to the graph.
2. Each neuron is represented by a single node called a computation node.
3. The communication links interconnecting the source and computation nodes of the graph carry no weight; they merely provide directions of signal flow in the graph.