Neural Networks As A Problem-solving Paradigm

The Paradigm:-

The generic characteristics of neural networksmake possible their use for:

• Function approximation, when a set of data is presented
• Pattern association
• Data clustering, categorization, and conceptualization
• Learning statistical parameters
• Accumulating knowledge through training
• "Extracting" knowledge through analysis of the connection weights
• Inserting knowledge in a neural network structure for the purpose of approximate reasoning

Neural network models provide massive parallelism, robustness, and approximate reasoning, which areimportant for dealing with uncertain, inexact, and ambiguous data, with ill-defined problems and sparsedata sets. All the above-mentioned points are discussed here. The problem-solving process, when usingneural networks, comprises two phase:-

(1) The training phase, when training examples are used for training a neural network, or rules are inserted in its structure.

(2) The recall phase, when new data are fed into the already trained network and a recall algorithm is used to calculate the results.

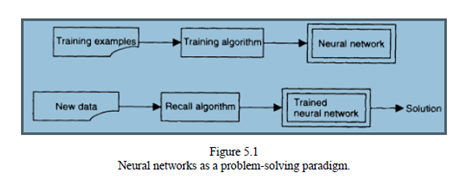Following the representation of the problem-solving process as mapping the domain space into the solution space,this process can be viewed here as mapping the problem domain space into an input state space of a neural network; mapping the solution space into an output space of the neural network; and mapping the problem knowledge into the synaptic space of all the connection weights of a neural network (or collection ofnetworks); the synaptic connection weights accommodate the problem knowledge.There are some general steps to follow when using neural networks as a problem-solving paradigm:-

1. Problem identification. What is the generic problem and what kind of knowledge is available?

2. Choosing an appropriate neural network model for solving the problem.

3. Preparing data for training the network, which process may include statistical analysis, discretization, and normalization.

4. Training a neural network, if data for training are available. This step may include creating a learning environment in which neural networks are "pupils."

5. Testing the generalization ability of the trained neural network and validating the results.

6. Optimizing the architecture, if necessary, which may require a repetition of some of the above steps until satisfactory validation results are obtained. Special strategies to improve the neural network performance may be needed.