Representing Spatial And Temporal Patterns In Neural Networks

Introduction:-Representing space and time is an important issue in knowledge engineering. Space can be represented in a neural network by:-

• Using neurons that take spatial coordinates as input or output values. Fuzzy terms for representing location, such as "above," "near," and "in the middle" can also be used.
   
• sing topological neural networks, which have distance defined between the neurons and can represent spatial patterns by their activations. Such a neural network is the SOM; it is a vector quantizer, which preserves the topology of the input patterns by representing one pattern as one neuron in the topological output map.

Representing time in a neural network can be achieved by:

• Transforming time patterns into spatial patterns.
   
• Using a "hidden" concept, an inner concept, in the training examples
  .
• Using an explicit concept, a separate neuron or group of neurons in the neural network, takes time moments as values.

Different connectionist models for representing "time" and the way they encode time are explained below

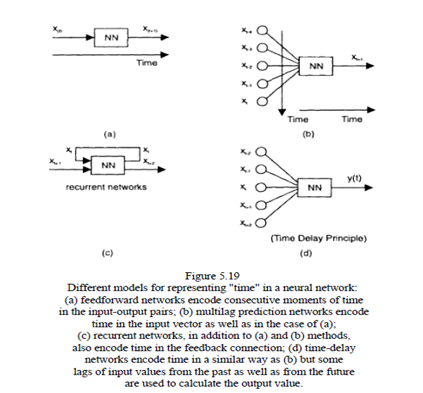
1. Feedforward networks may encode consecutive moments of time as input-output pairs.

2. Multiage prediction networks encode time in the input vector as well as in the case of (1).

3. Recurrent networks, in addition to (1) and (2), also encode time in the feedback connection.

4. Time-delay networks encode time in a similar way as (2) but some lags of input values from the past as well as from the future are used to calculate the output value.

An interesting type of a neuron, which can be successfully used for representing temporal patterns, is the leaky integrator. The neuron has a binary input, a real-valued output, and a feedback connection. The output (activation) function is expressed as:

y(t 1) = x(t), if x is present, or

y(t 1) = f(y(t)), if x is not present,

Where the feedback function is usually an exponential decay. So, when an input impulse is present (i.e. = 1), the output repeats it (y = 1). When the input signal is not present, the output value decreases overtime, but a"track" of the last input signal is kept at least for some time intervals. The neuron "remembers" an event x for some time, but "forgets" about it in the distant future. A collection of leaky integrators can be used, each representing one event happening over time, but all of them able to represent complex temporal patterns of time correlation between events. If another neural network, for example, ART, is linked to the set of leaky integrators, it can learn dynamic categories, which are defined by time correlation between the events.