The Hopfield Network
Introduction:-Hopfield networks, named after their inventor John Hopfield (1982), are fully connected feedback Networks. The neurons in Hopfield networks are characterized by the following: binary or bivalent input signals, binary or bivalent output signals, simple summation function, and hard-limited threshold activation function. There are alternative variants of realizations of a Hopfield network. Every neuron j, j = 1, 2, . . .,n in the network is connected back to every other one, except itself. Input patterns xj are supplied to the external inputs Ij and cause activation of the external outputs.
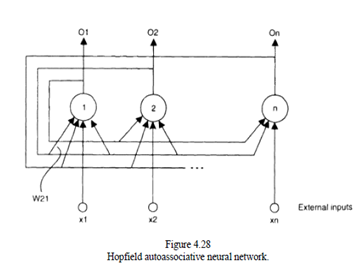 The response of such a network, when an input vector is supplied during the recall procedure, is dynamic, that is, after supplying the new input pattern, the network calculates the outputs and then feeds them back to the neurons; new output values are then calculated, and so on, until an equilibrium is reached.
The response of such a network, when an input vector is supplied during the recall procedure, is dynamic, that is, after supplying the new input pattern, the network calculates the outputs and then feeds them back to the neurons; new output values are then calculated, and so on, until an equilibrium is reached.
Equilibrium is considered to be the state of the system when the output signals do not change for two consecutive cycles, or change within a small constant. The weights in a Hopfield network are symmetrical for reasons of stability in reaching equilibrium, that is, wij = wji. The network is of an additive type, that is,
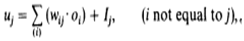
Where oj = 1 if uj > Qj (threshold for the jth neuron); oj = 0 if uj < Qj; and oj is unchanged if uj = Qj.The training procedure for a Hopfield network is reduced to a simple calculation of the weights wij on the basis of the training examples with the use of the formula:
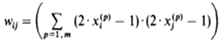
Where the summation is held for all the training patterns x(p),xi(p) is the ith binary value of the input pattern p; and the expressions in parentheses can be only 1 or 0 according to the value of the input pattern. An interesting characteristic of the weights wij is that they measure the correlation between the frequencies of firing of neurons i and j over the full set of examples. It is a variant of the Hebbian learning law, that is, the connection weights increase if two adjacent nodes fire simultaneously.

It can be organized in the following modes:
- Asynchronous updating: Each neuron may change its state at a random moment with respect to the others.
- Synchronous updating: All neurons change their states simultaneously at a given moment.
- Sequential updating: Only one neuron changes its state at any moment; thus all neurons change their states, but sequentially.