The Nps Architecture

An NPS is a "pure" connectionist system. A concrete NPS system is constructed for each defined set of production rules. An NPS consists of three neural sub networks:

(1) Production memory (PM);

 (2) Working memory (WM); and

(3) Variable binding space (VBS).

The PM contains r neurons, where r = r₁ r₂ is the total number of rules (productions), r₁the number of productions with variables, and r₂ the number of productions without variables. Only one variable is allowed in a rule. All the facts held in the WM have the form of attribute-value pairs. WM is a matrix of v_x a neurons, where a is the number of attributes and v is the number of their possible values. Each neuron in the WM corresponds to one fact, either Boolean, or fuzzy proposition.

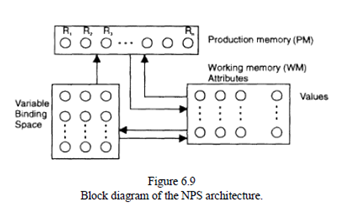VBS is a matrix of v × r₁ neurons. Each column of this matrix corresponds to one production with a variable, and each row to one of v possible values of the variables. The PM and the VBS form one attractor neural network and the WM provides the external inputs to its neurons. The inference cycle of an NPS is similar to the cycle of the classic symbolic production systems, but it is implemented in a connectionist way. Here, the match and select parts of the "recognize" phase are mixed, which is different when compared with the symbolic production systems. The act phase consists of updating the WM after opening two gates, one from the PM and another from the VBS. Simple propositional "true/false" rules can be realized as an NPS system:

R_i: IF C1 AND C2. . . and C_n THEN A1,A2,. . .,Am, where C_i, i = 1, 2,. . . , n, are "true/false" condition elements and A_j,j = 1, 2,. . . , m, are actions of the form of "assert"/"retract" a proposition in the working memory. For these kinds of simple production rules, the connection weights of the attractor network can be calculated in such a way that each rule is considered to be a "pattern," a stable attractor. During the match phase, when the facts in the WM match the production memory, the PM network goes into an equilibrium state after several iterations, which state is an attractor representing one rule. Then the activated rule (a neuron in the PM) updates the WM according to its consequent part (asserts or deletes propositions). The propositions (the facts) are represented by activation values of 0 and 1 of the neurons in the WM.

The PM always converges into a stable state representing a rule when input values are supplied to exactly match the condition elements in the rule. NPS can realize any production system that consists of propositional rules. The inference results are equivalent to those, produced by the built-in inference in a production language (e.g., CLIPS).

The existence of a huge amount of spurious states in attractor neural networks, which may cause a local minima problem, can be used for approximate reasoning when the facts can have any truth value between 0 and 1; therefore the condition elements in a rule are partially matched. In this case, the attractor PM network will relax in a spurious state, which means that more than one rule may get activated to a certain degree. The WM then can be updated either by the rule with the highest level of activation (sequential updating), or by all the rules, which level of activation is above a threshold (parallel updating). Using partial match for approximate reasoning in an NPS is a very strong point, which makes an NPS applicable to solving difficult A1 problems

In general, production rules to be realized in an NPS can have the following form:

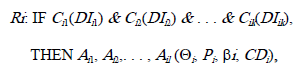
Where C_ij are condition elements of the form of attribute-value pairs representing boolean or fuzzy propositions of the type “attribute is value ," or their negation; DI_ij is a relative degree of importance of the i_j-th condition element C_ij; and A_ij is one of the actions insert or delete a fact in the WM. Four inference control coefficients (Q_i, P_i, b_i,CD_i) may be attached to every production. Q_iis a threshold which determines the noise tolerance. The lower the value of Q_i, the greater the noise tolerance, but at the same time, the greater the possibility of erroneous activation of the rule. P_i is a data sensitivity factor which controls the sensitivity of the rule R_itoward the presence of relevant facts. Q_i and P_i control the partial match in NPS. b_iis a reactiveness factor for the rule R_i. It regulates the activation of the rule R_i depending on how much it is matched by the current facts in the working memory.

NPS has two modes of representing facts in the production rules and in the WM, respectively (1) without negated condition elements, and (2) with negated condition elements.