Using Training Samples

Introduction: -After successful learning it is particularly interesting whether the network has only memorized – i.e. whether it can use our training samples to quite exactly produce the right output but to provide wrong answers for all other problems of the same class.

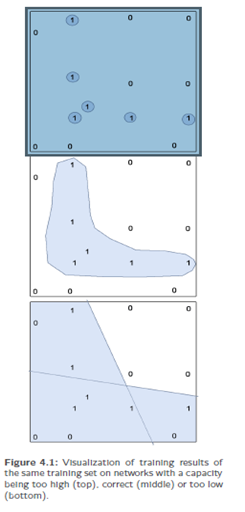
Suppose that we want the network to train a mapping 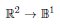and therefore use the training samples from fig. 4.1: Then there could be a chance that, finally, the network mwill exactly mark the colored areas around the training samples with the output and otherwise will output 0. Thus, it has sufficient storage capacity to concentrate on the six trainingsamples with the output 1. This impliesan oversized network with too much freestorage capacity.

On the other hand a network could have insufficient capacity this rough presentation of input data does not correspond to the good generalization performance we desire. Thus, we have to find the balance.

It is useful to divide the set of training samples:-An often proposed solution for these problems is to divide, the training set into one training set really used to train and one verification set to test ourprogress provided that there are enough training samples. The usual division relations are, for instance, 70% for training data and 30% for verification data. We can finish the training when the network provides good results on thetraining data as well as on the verification data.

If the verification data provide poor results, do not modify the network structure until these data provide good results otherwise you run the risk of tailoring the network to the verification data.This means, that these data are includedin the training even if they are not used explicitly for the training. The solution is a third set of validation data used only for validation after a supposably successful training. By training less patterns, we obviously withhold information from the network and risk to worsen the learning performance.

But this text is not about 100% exact reproduction of given samples but about successful generalization and approximation of a whole function – for which it can definitely be useful to train less information into the network.

Order of pattern representation: -If patterns are presented in random sequence, there is no guarantee that the patterns are learned equally well (however, this is the standard method). Always the same sequence of patterns, on the other hand, provokes that the patterns will be memorized when using recurrent networks. A random permutation would solve both problems, but it is very time consuming to calculate such a permutation.