Composite Trapezium Rule

Composite trapezium rule : Suppose that the interval [a, b] is subdivided into M subintervals [x_k , x_{k 1}] of width h = (b−a)/M by using the equally spaced nodes x_k = a kh, for k = 0, 1, . . . , M. The composite trapezoidal rule forM subintervals can be expressed in any of three equivalent ways

1. 

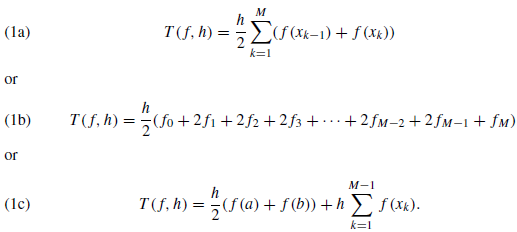
This is an approximation to the integral of f (x) over [a, b], and we write

2.

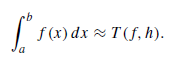
Proof. Apply the trapezoidal rule over each subinterval [x_k-1, x_k ]. Use the additive property of the integral for subintervals

3.

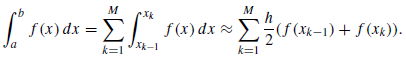
Since h/2 is a constant, the distributive law of addition can be applied to obtain (1a). Formula (1b) is the expanded version of (1a). Formula (1c) shows how to group all the intermediate terms in (1b) that are multiplied by 2.

Approximating f (x) = 2 sin(2√x) with piecewise linear polynomials results in places where the approximation is close and places where it is not. To achieve accuracy, the composite trapezoidal rule must be applied with many subintervals. In the next example we have chosen to integrate this function numerically over the interval [1, 6]. Investigation of the integral over [0, 1] is left.

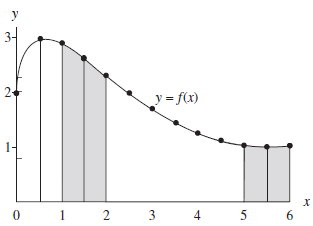
                                                     Figure : Approximating the area under the curve y = 2 sin(2√x)with the composite trapezoidal rule.