Direct Method For Solving Linear System

Direct methods produce the exact solution after a finite number of steps (disregarding the round-off errors). In these methods, we can determine the total number of operations (additions, subtractions, divisions and multiplications). This number is called the operational count of the method.

Direct Methods:  If the system of equations has some special forms, then the solution is obtained directly. We consider two such special forms

(a) Let A be a diagonal matrix, A = D. That is, we consider the system of equations.

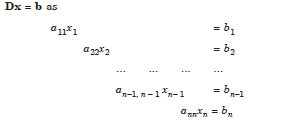.....................1.1             

 

This system is called a diagonal system of equations. Solving directly, we obtain

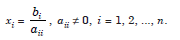...........................1.2

 

(b) Let A be an upper triangular matrix, A = U. That is, we consider the system of equations Ux = b as

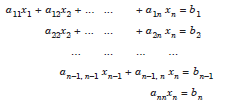....................1.3

 

This system is called an upper triangular system of equations. Solving for the unknowns in the order xn, xn–1, ..., x1, we get

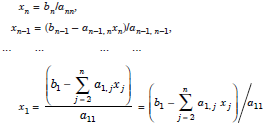.........................1.3

 

1. The unknowns are obtained by back substitution and this procedure is called the back substitution method.
2. Therefore, when the given system of equations is one of the above two forms, the solution is obtained directly.

Before we derive some direct methods, we define elementary row operations that can be performed on the rows of a matrix.

Elementary row transformations (operations):  The following operations on the rows of a matrix A are called the elementary row transformations (operations).

(i) Interchange of any two rows. If we interchange the ith row with the jth row, then we usually denote the operation as Ri ↔ Rj.

(ii) Division/multiplication of any row by a non-zero number p. If the ith row is multiplied by p, then we usually denote this operation as pRi.

(iii) Adding/subtracting a scalar multiple of any row to any other row. If all the elements of the jth row are multiplied by a scalar p and added to the corresponding elements of the ith row, then, we usually denote this operation as Ri ← Ri pRj. Note the order in which the operation Ri pRj is written. The elements of the jth row remain unchanged and the elements of the ith row get changed.

These row operations change the form of A, but do not change the row-rank of A. The matrix B obtained after the elementary row operations is said to be row equivalent with A. In the context of the solution of the system of algebraic equations, the solution of the new system is identical with the solution of the original system.

The above elementary operations performed on the columns of A (column C in place of row R) are called elementary column transformations (operations). However, we shall be using only the elementary row operations.

In this section, we derive two direct methods for the solution of the given system of equations, namely, Gauss elimination method and Gauss-Jordan method.