Eigen Value Problems

Eigen value :  A scalar associated with a given linear transformation of a vector space and having the property that there is some nonzero vector which when multiplied by the scalar is equal to the vector obtained by letting the transformation operate on the vector; especially : a root of the characteristic equation of a matri.The concept of eigen values and finding eigen values and eigen vectors of a given matrix are very important for engineers and scientists.

The classical mathematical eigenvalue problem is defined as the solution of the following equation:

......................1.1

 

The N by N A matrix is real and symmetric; however, it may be singular and have zero eigenvalues λ_n . A typical eigenvector v_n has the following orthogonality
properties:

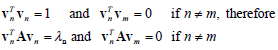.................1.2

If all eigenvectors V are considered the problem can be written as

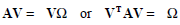.....................1.3

There are many different numerical methods to solve Equation (1.3) for eigenvectorsV and the diagonal matrix of eigenvalues Ω. In structural analysis, in
general, it is only necessary to solve for the exact eigenvalues of small systems. Therefore, the most reliable and robust will be selected since the computational time will always be relatively small. For the determination of the dynamic mode shapes and frequencies of large structural systems subspace iteration or Load Dependent Ritz, LDR, vectors are the most efficient approaches.

SOLUTION OF THE GENERAL EIGENVALUE PROBLEM:

The general eigenvalue problem is written as

AV = BVΩ................1.4

where both A and B are symmetrical matrices. The first step is to calculate the eigenvectors  V_B of the B matrix. We can now let the eigenvectors V be a linear
combination or the eigenvectors of the B matrix. Or,

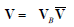...................1.5

Substitution of Equation (1.5) into Equation (1.4) and the pre multiplication of both sides by V_B^T yields

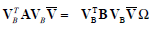....................1.6

If all eigenvalues of the B matrix are nonzero the eigenvectors can be normalized so that V_B^TBV_B=I. Hence, Equation (1.6) can be written in the following classical form:

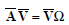.....................1.7

where

                                                                                                                                  

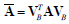
Therefore, the general eigenvalue problem can be solved by the application of the Jacobi algorithm to both matrices. If the B matrix is diagonal the eigenvectors V_B matrix will be diagonal with the diagonal terms equal to 

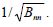
This is the case for a lumped mass matrix. Also, mass must be associated with all degrees-of-freedom and all eigenvectors and values must be calculated.